Ellipses

L’étude du mouvement des astres conduit souvent à une trajectoire elliptique. Les aspects physiques de cette orbite sont succintement présentés dans le chapitre 7 de T S. Cette page ne traitera donc que des aspects géométriques de cette remarquable courbe. Les formules sont données en vrac, mais quelques indices permettent de refaire les démonstrations.

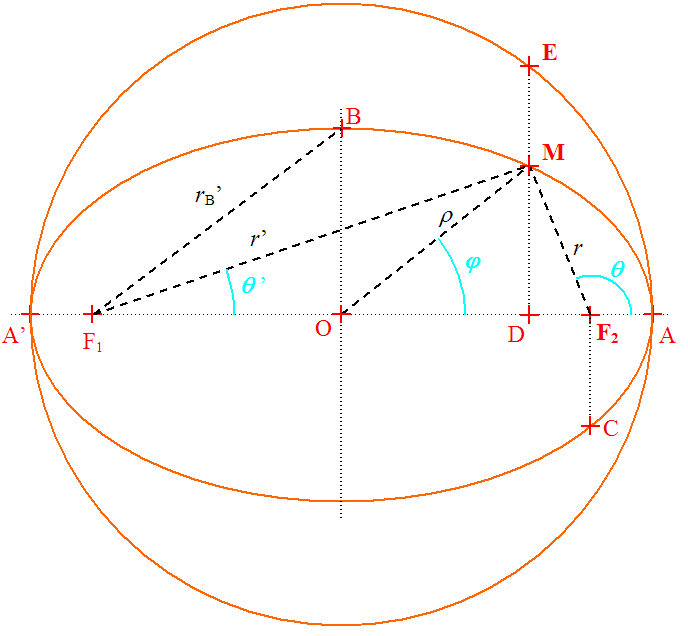
a : demi grand axe

b : demi petit axe

e : excentricité

p : paramètre

e : coefficient d’aplatissement

a = OA = OA’ = 5,000 cm

b = OB = 3,000 cm

cos q_C = 0 Þ F₂C = p

r_B·cos (p - q_B) = a·e Þ cos q_B = -e Þ F₂B = F₁B = a

Pythagore dans F₁DM et DF₂M Þ r’ - r = 2·e·x (x = OD)

… = (r + r’) - (r’ - r) = … Þ r = a - e·x

Pythagore dans DF₂M Þ (x/a)² + (y/b)² = 1 Þ x = a·cos t = r·cos j & y = b·sin t = r·sin j