Le poids
La réaction du support
La poussée d’Archimède
Les forces de frottement fluide
Les forces de frottement solide
Les forces électriques
Les forces gravitationnelles
Les forces magnétiques
Les forces pressantes
Les forces de tension
Pour un objet macroscopique, on tient toujours compte du poids 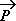 mais pour une particule (électron, proton...) on peut le négliger sans problème.
mais pour une particule (électron, proton...) on peut le négliger sans problème.
 La définition du poids est une relation vectorielle :
La définition du poids est une relation vectorielle : 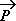 = m·
= m·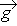 .
.
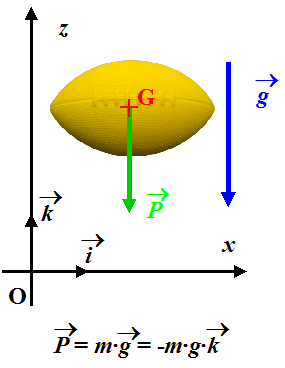
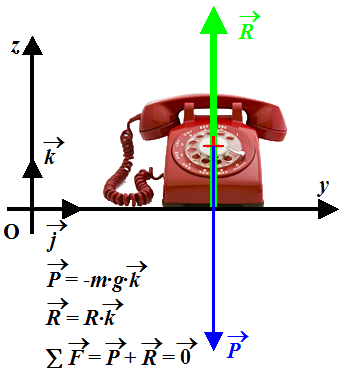
Une figure permet de mieux fixer les idées :
On obtient alors 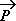 = -m·g·
= -m·g· .
La plupart du temps, le centre de gravité est facile à trouver. Mais parfois, il peut se trouver à l’extérieur du corps :
.
La plupart du temps, le centre de gravité est facile à trouver. Mais parfois, il peut se trouver à l’extérieur du corps :
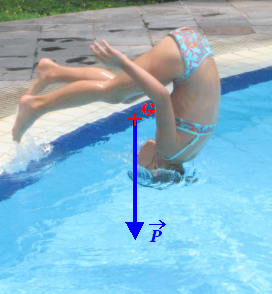
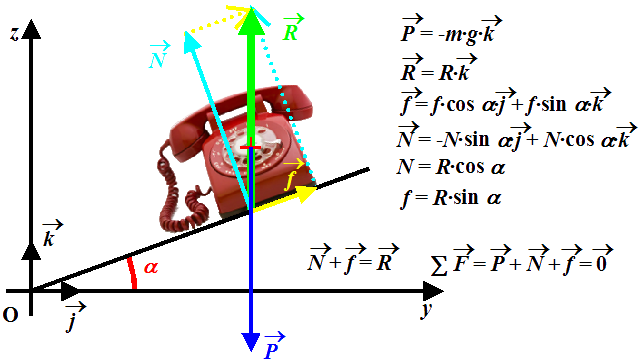
Là où les choses se compliquent un peu, c’est pour un objet dont la masse n’est pas équitablement répartie, son centre d’inertie ne correspond plus à un barycentre géométrique (le moteur est plus lourd que le coffre et son contenu). Deuxième difficulté, si les axes du repère de projection ne sont pas horizontaux et verticaux : 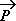 = - Px·
= - Px· - Py·
- Py·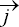 .
.

Ce qui donne alors : 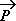 = - m·g·sin a·
= - m·g·sin a· - m·g·cos a·
- m·g·cos a·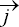 . Les deux signes moins sont parfaitement logiques étant donné l’orientation du repère.
. Les deux signes moins sont parfaitement logiques étant donné l’orientation du repère.
Autre petite subtilité, quand on représente le poids sur une figure, on observe toujours l’objet de profil et jamais de dessus...

 = -R·
= -R·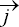 et
et 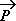 = P·
= P·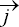 .
.
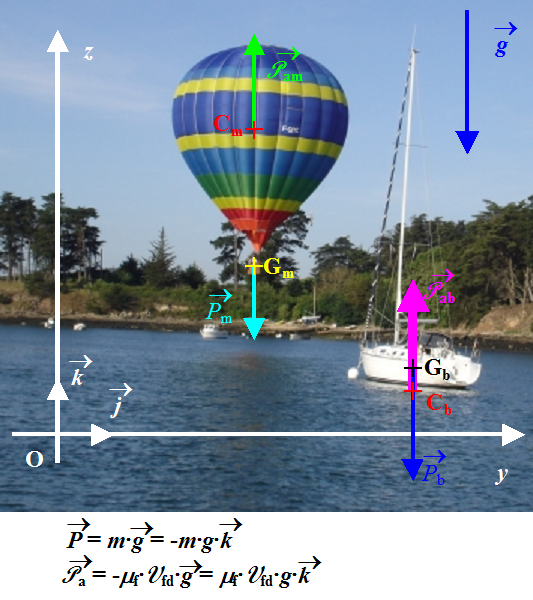
La poussée d’Archimède s’applique sur le centre de carène C qui n’est rien d’autre que le centre de gravité du fluide déplacé. Rappelons ce théorème bien connu : « Tout corps plongé entièrement ou partiellement dans un fluide, subit de sa part une poussée opposée au poids de fluide déplacé ». Cette poussée est donc verticale, dirigée vers le haut et sa norme se calcule par Pa = mf·Vfd·g.
Pour un navire, C est en-dessous de G donc celui-ci peut chavirer. Pour une montgolfière, C est au-dessus de G donc celle-ci ne peut chavirer.

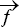 = fx·
= fx· - fy·
- fy·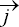 = -l·
= -l· (l peut avoir une forme très complexe et ne pas juste se résumer à une constante — petit exo : prouver que l s’exprime en kg/s).
(l peut avoir une forme très complexe et ne pas juste se résumer à une constante — petit exo : prouver que l s’exprime en kg/s).

Les frottements s’opposent au mouvement, et pourtant sans eux nous n’irions pas loin :

Sur cette photo, la personne se déplace suivant 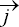 , le monocycle se déplace suivant
, le monocycle se déplace suivant 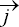 mais les forces de frottements sont aussi orientés suivant
mais les forces de frottements sont aussi orientés suivant 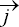 , alors ? Regardons le mouvement de la roue de plus près, son sens de rotation est indiqué et au niveau du point B, le vecteur vitesse
, alors ? Regardons le mouvement de la roue de plus près, son sens de rotation est indiqué et au niveau du point B, le vecteur vitesse  d’un point du pneu est orienté suivant -
d’un point du pneu est orienté suivant -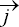 . Les frottements s’opposent au mouvement, ils seront donc orientés suivant
. Les frottements s’opposent au mouvement, ils seront donc orientés suivant 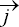 .
.

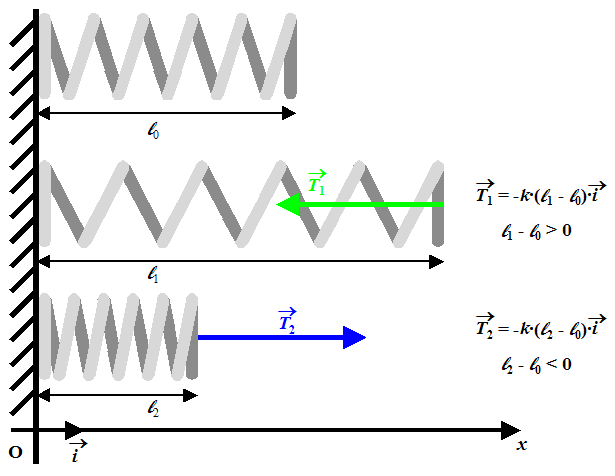
Tous ces objets respectent la loi de Hooke : T = -k·Dl. Dl = l - l0 représente l’allongement de l’objet, l sa longueur à un instant donné en mètre (m), l0 sa longueur à vide en mètre (m), k sa raideur en newton par mètre (N/m) et T la tension en newton (N).
Pour les cordes, les chaînes, les courroies... l’allongement est toujours positif mais très faible (quelques micromètres), la raideur est très grande (de l’ordre de 107 N/m), la tension est toujours dirigée vers l’intérieur de la corde.
Pour les ressorts, la raideur balaye une large gamme (de quelques newtons par mètre à quelques dizaines de milliers de newtons par mètre). L’allongement sera une grandeur algébrique : positive, la tension sera dirigée vers l’intérieur du ressort (travail en traction) mais négative, la tension sera dirigée vers l’extérieur du ressort (travail en compression).
Il suffit de retenir que la tension est une force que génèrent l’élastique et le ressort pour reprendre durablement leur forme au repos.