en cours
Le pendule
L’oscillateur harmonique
Les oscillations forcées
Liens externes
The player will show in this paragraph
Ici 3·T = 4,167 s c à d T = 1,39 s pour L = 48 cm = 0,48 m.
Le traitement des données permet d’obtenir la relation T2/L = k avec k = 4,0 s2·m-1, on peut aussi écrire k = a2 avec a = 2,0 s·m-1/2.Avec un peu d’astuce, on se rend compte que derrière ces deux constantes se cachent 2, p et g = 9,81 N/kg = 9,81 m·s-2.
Calculons g-1 = 0,102 s2·m-1, la même unité que k.
Calculons g1/2 = 3,13 m1/2·s-1, 3,13 ! Tic tac, tic tac, ce nombre me fait penser à p.
Calculons p/g1/2 = 1,00 s·m-1/2 ! On s’approche de a.
Calculons 2·p/g1/2 = 2,01 s·m-1/2 = a.
Calculons 4·p2/g = 4,02 s2·m-1 = k.
Au final, on obtient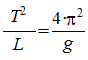 
ou 
.
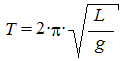On en tire le graphique suivant :
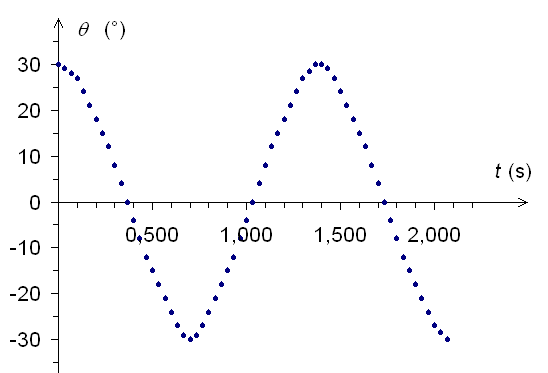
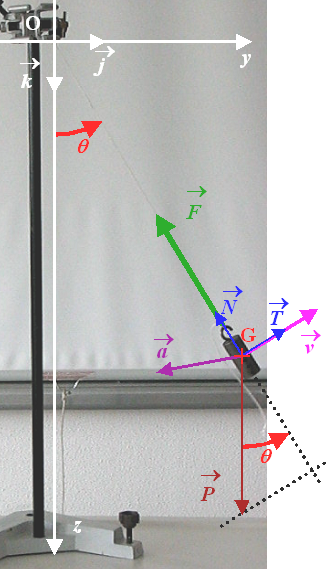
La masselotte est soumise à deux forces, dans le repère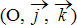 
:
– le poids 
;
– la tension du fil 
.
Ce qui donne 
Dans le référentiel du laboratoire supposé galiléen, Newton2 nous indique que 
.
Ici 
avec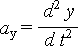 
, 
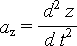et y = L·sin q et z = L·cos q.
Maintenant pour poursuivre, je vous souhaite bien du courage ;-) la raison en est simple, le repère 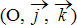n’est pas du tout adapté à cette étude… Heureusement, nous connaissons le repère de Frenet 
:
– le poids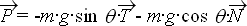 
;
– la tension du fil 
;
– l’accélération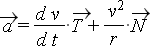 
.
avec 
d’où 
.
Dans le référentiel du laboratoire supposé galiléen, Newton2 nous indique que . Cette relation, projetée suivant le vecteur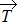 
, nous donne alors : 
.
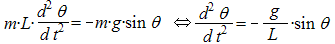On obtient une équation différentielle un peu compliquée à résoudre sauf si on se limite à des angles de faibles valeurs*. Dans ce cas sin q » q et on obtient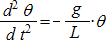 
.
* Qu’est-ce qu’un angle de faible valeur ? Regardons sin (10°) » 0,17 raté ! Alors plus petit, sin (1°) » 0,017 raté ! Encore plus petit, sin (0,1°) » 0,001 7 encore raté ! Essayons autre chose : sin (0,1 rad) » 0,099 ah ! et plus grand, sin (0,5 rad) » 0,48 et encore plus grand, sin (1 rad) » 0,84. La relation sin q » q ne fonctionne que pour des angles exprimés en radians, la valeur limite pour la validité de cette relation sera de 0,5 rad.
La solution de l’équation est q = q0·cos (w·t) avec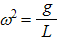 
où w est la pulsation.
La fonction cosinus est périodique : cos (w·t) = cos (w·t + 2·p) = cos (w·(t + 2·p/w)) = cos (w·(t + T)) avec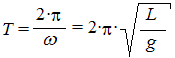 
qui est la période des oscillations.
On peut aussi écrire .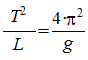
The player will show in this paragraph
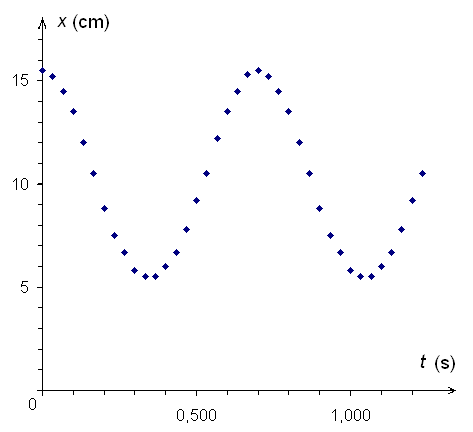
Ici 7·T = 5,00 s c à d T = 0,714 s pour m = 200 g = 0,200 kg.
La constante de raideur du ressort vaut k = 15,5 N·m-1 = 15,5 kg·m·s-2·m-1 = 15,5 kg·s-2.Pour faire disparaître les “s-2”, essayons k·T2 = 7,90 kg.
Pour faire disparaître les “kg”, essayons k·T2/m = 39,5.
Dans le cas du pendule simple, 4·p2 était apparu, regardons : 4·p2 = 39,5 oh !
On peut donc écrire T2·k = 4·p2·m.
On en tire le graphique suivant :
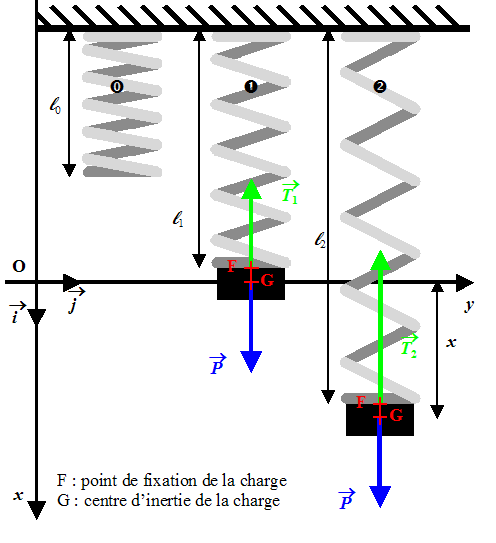
Œ : ressort à l’équilibre avec une charge de masse m. Mais le système étudié sera la charge :
– le poids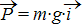 
;
– la tension du ressort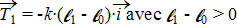 
.
.
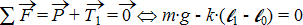: la charge est déplacée temporairement de sa position d’équilibre par une force extérieure, ce qui provoque la mise en oscillations du système :
– le poids ;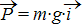
– la tension du ressort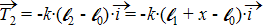 
parce que le repère 
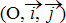n’est pas choisit au hasard ;
– la somme des forces 
en utilisant ce qui a été vu en Œ.
.
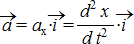Dans le référentiel du laboratoire supposé galiléen, Newton2 nous indique que .
Cette relation, projetée suivant le vecteur 
, nous donne alors : 
.
La solution de cette équation est x = x0·cos (w·t) avec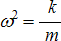 
où w est la pulsation.
La fonction cosinus est périodique : cos (w·t) = cos (w·t + 2·p) = cos (w·(t + 2·p/w)) = cos (w·(t + T)) avec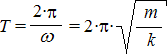 
qui est la période des oscillations.