Chapitre 7    Mouvements autour des astres

en cours


Le système solaire
La force d’attraction gravitationnelle
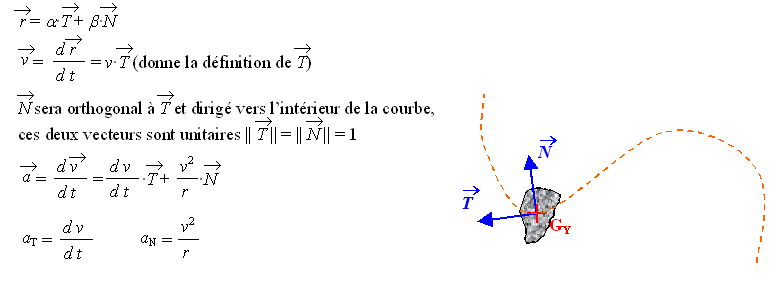
Le repère de Frenet
Étude simplifiée du mouvement
Quelques éléments sur l’étude générale

L’activité 12.3 de 2nde peut être traitée en guise d’introduction.

Le système solaire

Source : Wikipédia

– Monsieur, vous travaillez mal !

– Je suis un novice !

Ceci pour retenir que nous avons dans l’ordre : Soleil, Mercure, Vénus, Terre, Mars, Jupiter, Saturne, Uranus et Neptune.

En prime, quelques informations sur ces astres :

Planète Réq (km) m (kg) T (j) a (km) e
Soleil 696 000 198 900 000·1022 - - -
Mercure 2 440 33·1022 87,97 57,91·106 0,205 630 69
Vénus 6 052 487·1022 224,70 108,21·106 0,006 773 23
Terre 6 378 597·1022 365,26 149,60·106 0,016 710 22
Mars 3 402 64·1022 686,96 227,94·106 0,093 412 33
Jupiter 71 492 189 900·1022 4 335,35 778,41·106 0,048 392 66
Saturne 60 268 56 850·1022 10 757,74 1 421,18·106 0,054 150 60
Uranus 25 559 8 681·1022 30 799,10 2 876,68·106 0,047 167 71
Neptune 24 961 10 240·1022 60 224,90 4 498,25·106 0,008 585 87

Réq représente le rayon de l’astre mesuré au niveau de son équateur, a est le demi grand axe de l’orbite et e son excentricité (plus d’info sur ces deux grandeurs dans la page sur les ellipses).

La force d’attraction gravitationnelle

Deux astres X et Y sont en interaction, ils s’attirent mutuellement mais bien évidemmment le plus léger gravite autour du plus lourd (mX > mY) :
G = 6,67·10-11 m3·kg-1·s-2, constante universelle de gravitation

mX et mY en kilogramme

r en mètre

Le repère de Frenet

I. Définition

II. Prédiction du type de mouvement

La conclusion est alors la suivante :

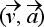– Î [0 ; p/2[ : mouvement accéléré ;

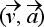– = p/2 : mouvement uniforme ;

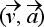– Î ]p/2 ; p] : mouvement décéléré.

Étude simplifiée du mouvement

Nous nous limiterons au cas particulier où Þ a = 0 & b = -r.

Dans un référentiel lié à l’astre X et supposé galiléen, on utilise la deuxième loi de Newton :

L’hypothèse simplificatrice nous conduit à une trajectoire circulaire. Les données sur les planètes du système solaire vont nous permettre d’infirmer ou de confirmer la validité de l’hypothèse :

Planète e (%)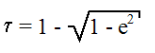
Mercure 0,205 630 69 21
Vénus 0,006 773 23 0,023
Terre 0,016 710 22 0,14
Mars 0,093 412 33 4,4
Jupiter 0,048 392 66 1,2
Saturne 0,054 150 60 1,5
Uranus 0,047 167 71 1,1
Neptune 0,008 585 87 0,037

t représente le “taux d’ellipticité”, plus il est faible plus on se rapproche du cercle, plus il est grand plus l’ellipse sera aplatie. Notre hypothèse est donc valable pour 7 planètes sur 8 !

Quelques éléments sur l’étude générale

I. Les quatres trajectoires

En réalité, quatre situations peuvent exister :

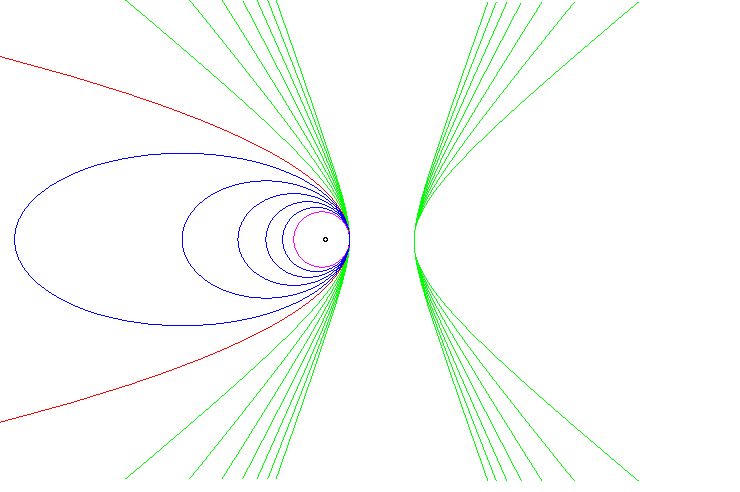
– trajectoire circulaire ;

– trajectoire elliptique ;

– trajectoire parabolique ;

– trajectoire hyperbolique.

II. L’orbite elliptique

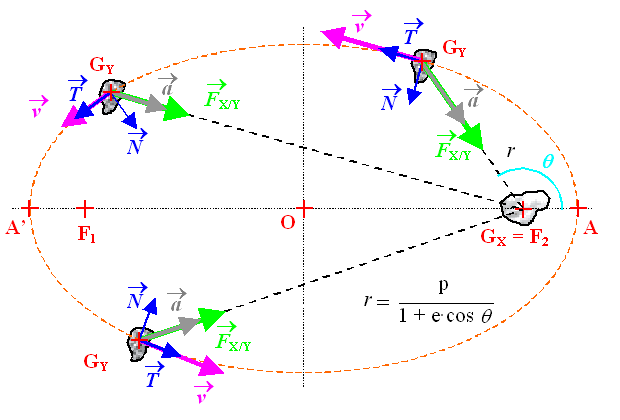
La moitié du temps, B est accéléré par la force gravitationnelle et l’autre moitié du temps, elle le ralentit.

Pour les curieux, j’ai ajouté une page sur les ellipses en mathématiques.

III. Les trois lois de Kepler (1618)

1ère loi de Kepler

Les planètes du système solaire décrivent des trajectoires elliptiques dont le Soleil occupe l’un des foyers.

2e loi de Kepler

Au cours de ce mouvement, le rayon vecteur Soleil-planète balaie des aires égales pendant des durées égales c à d si DtEG = DtHJ alors A1 = A2.

3e loi de Kepler

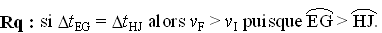
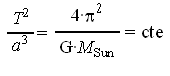Le rapport du “carré de la période de révolution” par le “cube du demi grand axe de l’orbite” est le même pour toutes les planètes c à d . La période de révolution T est la durée nécessaire pour parcourir toute l’ellipse ; a = [OA] = [A’A]/2, pour l’orbite circulaire [OF2] = 0 d’où r = [OA] = [F2A].