

La chute libre
La chute dans un fluide
 Dans ce cas, il n’y a qu’une seule force : le poids
Dans ce cas, il n’y a qu’une seule force : le poids 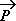 (soit un suppose que le mouvement se déroule dans le vide, soit on suppose que la poussée d’Archimède et les forces de frottements peuvent être négligés).
Seconde contrainte, la vitesse initiale doit être verticale :
(soit un suppose que le mouvement se déroule dans le vide, soit on suppose que la poussée d’Archimède et les forces de frottements peuvent être négligés).
Seconde contrainte, la vitesse initiale doit être verticale : 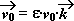
1. La gomme est le système étudié.
2. L’expérience se déroule dans une pièce (le laboratoire), on étudie alors le mouvement dans le référentiel du laboratoire supposé galiléen car l’expérience ne durera que quelques secondes.
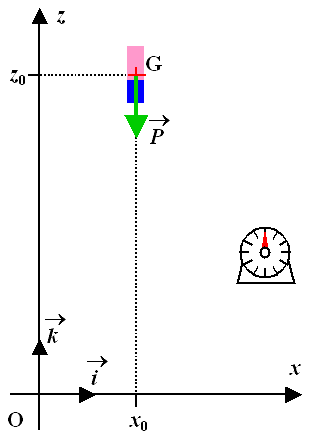
3. Le repère d’espace sera (O,  ,
,  ) où O est placé au niveau du sol (voir figure) ; le repère de temps sera une horloge ou un chronomètre qui se déclenche au moment où on lâche (lance) la gomme (t0 = 0).
) où O est placé au niveau du sol (voir figure) ; le repère de temps sera une horloge ou un chronomètre qui se déclenche au moment où on lâche (lance) la gomme (t0 = 0).
4. Il n’y a qu’une seule force : le poids  .
.
5. Dans la base ( ,
,  ) :
) : 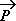 = m·
= m· = -m·g·
= -m·g· .
.
6. La seconde loi de Newton nous donne alors  et après simplification
et après simplification  .
.
| 7. | En projection sur l’axe (O, z) : az = -g | et sur l’axe (O, x)z: ax = 0. | |
| 8. | En intégrant une première fois : vz = -g·t + v0z = -g·t + e·v0 | et vx = v0x = 0 | |
| 9.zz | En intégrant une seconde fois : z = -1/2·g·t2 + e·v0·t + z0 | et x = x0 |
 Cette fois, la poussée d’Archimède et les forces de frottements ne sont plus négligés. On ne s’accordera qu’une seule simplification, à savoir v0 = 0.
Cette fois, la poussée d’Archimède et les forces de frottements ne sont plus négligés. On ne s’accordera qu’une seule simplification, à savoir v0 = 0.1. La gomme est le système étudié.
2. L’expérience se déroule dans une pièce (le laboratoire), on étudie alors le mouvement dans le référentiel du laboratoire supposé galiléen car l’expérience ne durera que quelques secondes.
3. Le repère d’espace sera (O,  ,
,  ) où O n’est plus placé au niveau du sol et l’axe (O, z) est maintenant orienté vers le bas (voir figure) ; le repère de temps sera une horloge ou un chronomètre qui se déclenche au moment où on lâche (lance) la gomme (t0 = 0).
) où O n’est plus placé au niveau du sol et l’axe (O, z) est maintenant orienté vers le bas (voir figure) ; le repère de temps sera une horloge ou un chronomètre qui se déclenche au moment où on lâche (lance) la gomme (t0 = 0).
4. Il y a trois forces : le poids 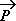 , la poussée d’Archimède
, la poussée d’Archimède 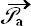 et les forces de frottements
et les forces de frottements 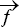 .
.
5. Dans la base ( ,
,  ) :
) : 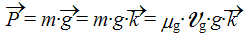 ;
;  * (la gomme est entièrement immergée) et
* (la gomme est entièrement immergée) et 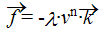 (la gomme tombe suivant
(la gomme tombe suivant  et les forces de frottements sont opposés au mouvement, ces frottements dépendent de la vitesse suivant une loi du type l·vn mais on n’en sait pas plus).
et les forces de frottements sont opposés au mouvement, ces frottements dépendent de la vitesse suivant une loi du type l·vn mais on n’en sait pas plus).
* g pour gomme et fd pour fluide déplacé
6. La seconde loi de Newton nous donne alors ![]()
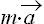 =
= 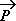 +
+ 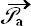 +
+  .
.
| 7.z | En projection sur l’axe (O, x)z: m·ax = 0 | |
| En intégrant une première fois : vx = v0x = 0 En intégrant une seconde fois : x = x0 En projection sur l’axe (O, z) : m·az = mg·Vg·g - mf·Vg·g - l·vn
En notant que
Comme m = mg·Vg, une nouvelle simplification apparait : Et maintenant... il ne faut pas espérer intégrer ceci donc on va feinter (utiliser la méthode d’Euler). |
| 8. | La méthode d’Euler
On effectue un changement de variables (A = g·(1 - mf/mg) et B = l/m) pour se retrouver avec
En se souvenant des cours de maths, on peut écrire
Maintenant, il faut transformer la fonction v(t) en une suite de type vp avec Dv = vp + 1 - vp pour obtenir Pour exploiter cette relation, il faut réaliser l’expérience pour obtenir des valeurs expérimentales de la vitesse puis utiliser un tableur pour affiner le modèle :
|
|
The player will show in this paragraph | Le fichier excel est à télécharger ici pour jouer à Euler's game |
La valeur de A peut être facilement calculée sans Euler puisque A = g·(1 - mf/mg).
Pour obtenir B et n, il suffit de superposer la courbe du modèle à la courbe expérimentale. n est sans unité mais B possède une unité un peu spéciale (m1-n·sn-2, amusez-vous à le démontrer !), raison pour laquelle on se contente souvent de marquer SI comme unité.