Principes
Le mouvement uniforme
Le mouvement uniformément varié
Position, vitesse et accélération
Cette étude doit être menée de manière rigoureuse :
1. Je définis le système, c’est l’objet étudié (voiture, bille, palet...).
2. Je choisis un référentiel, par rapport auquel l’objet se déplace (ou non). La fiche méthode 7 présente quelques référentiels.
3. Je choisis pour ce référentiel, un repère d’espace (O, 
, 
, 
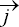) et un repère de temps (O, t).
4. J’effectue un bilan des forces qui agissent sur le système : 
Pour se simplifier la vie, on considère que toutes les forces agissent au niveau du centre d’inertie (qu’on appelle aussi centre de masse ou centre de gravité). La fiche méthode 8 traite des points d’application ainsi que des forces les plus courantes.
5. J’exprime ces vecteurs force en fonction des vecteurs de la base (, , ).
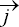6. Je suppose que le référentiel est galiléen et donc j’applique la deuxième loi de Newton : 
. m est la masse du système et 
est le vecteur accélération du centre d’inertie du système.
7. La deuxième loi de Newton est une relation vectorielle (regardez il y a des petites flèches...), maintenant je n’ai qu’une seule envie, c’est de me débarrasser de ces flèches et là ATTENTION aux erreurs ! La relation vectorielle doit être projettée sur des axes (voir fiche méthode 8).
Pour un mouvement à une dimension, je me retrouve avec une équation du type ax = ...
Pour un mouvement à deux dimensions, je me retrouve avec une équation du type ax = ... et ay = ...
Pour un mouvement à trois dimensions, je me retrouve avec une équation du type ax = ..., ay = ... et az = ...
8. Avec un peu de travail (il faut intégrer et tenir compte des conditions initiales), j’obtient vx, vy et vz (les composantes du vecteur vitesse 
du centre d’inertie).
).
est constante, celà ne présage rien sur sa direction ou son sens !) :
|
ax = 0 vx = v0x x = v0x·t + x0
|
ay = 0 vy = v0y y = v0y·t + y0
|
az = 0 vz = v0z z = v0z·t + z0
|
est constante, celà ne présage rien sur sa direction ou son sens !) :
|
ax = a0x vx = a0x·t + v0x x = 1/2·a0x·t2 + v0x·t + x0
|
ay = a0y vy = a0y·t + v0y y = 1/2·a0y·t2 + v0y·t + y0
|
az = a0z vz = a0z·t + v0z z = 1/2·a0z·t2 + v0z·t + z0
|
Sans trop de difficultés, on peut vérifier que vx2 - v0x2 = 2·a0x·(x - x0), ce qui fait normalement penser au théorème de l’énergie cinétique.
, et . indique où se trouve le centre d’inertie G, et indiquent comment il se déplace.
Ces trois vecteurs sont intimement liés : 
et 
.